2.1 概述
土的渗透性是指水流过土中孔隙的难易程度,是土的重要工程性质之一。
2.1.1 渗透现象
水在重力或其他应力作用下,通过土中孔隙流动的现象称为渗透。
2.1.2 渗透性在工程中的意义
- 地下水位的升降和变化
- 基坑开挖中的排水和降水
- 堤坝和挡土墙的渗流稳定
- 地基的固结沉降
- 地下工程的防水和排水
2.2 达西定律
达西定律是描述水在多孔介质中渗流的基本规律。
2.2.1 达西试验
1856年,法国工程师达西通过试验研究了水流过砂土的规律,得出了渗流速度与水力梯度之间的线性关系。
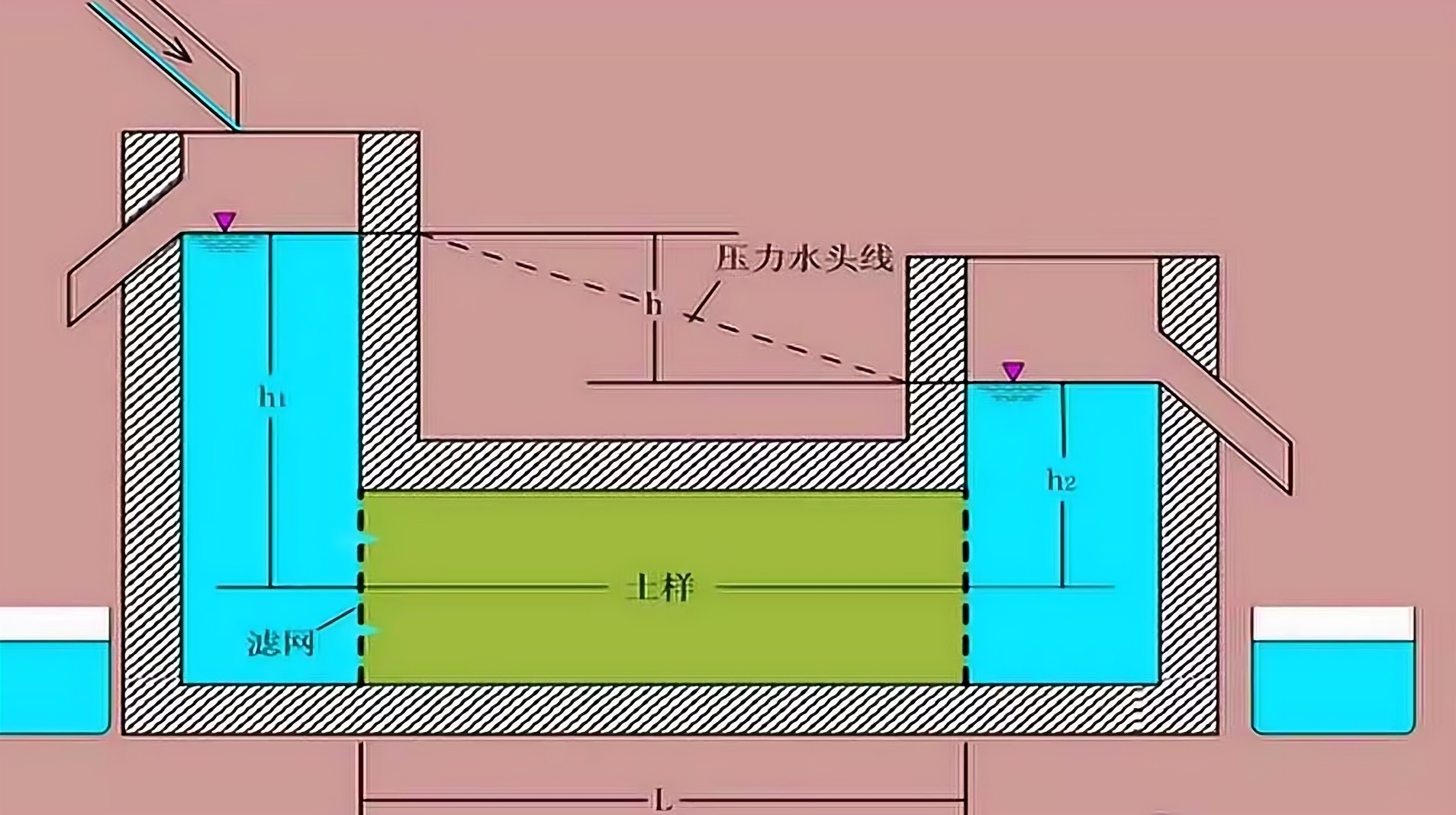
图2.1 达西定律试验装置示意图
2.2.2 达西定律的表达式
达西定律可以表示为:
v = k·i
其中:
- v:渗流速度(m/s),即单位时间内通过单位面积的水量
- k:渗透系数(m/s),反映土的透水能力
- i:水力梯度,即沿渗流方向单位长度上的水头损失
2.2.3 达西定律的适用范围
达西定律适用于层流状态下的渗流,即雷诺数Re ≤ 1的情况。
Re = vd/ν
其中:
- d:土颗粒的有效粒径(m)
- ν:水的运动粘滞系数(m²/s)
注意
对于粗颗粒土(如砾石、卵石等),当水流速度较大时可能发生紊流,此时达西定律不再适用。
2.3 渗透系数的测定
2.3.1 实验室测定方法
实验室中测定渗透系数的方法主要有:
- 常水头试验:适用于渗透性较大的土(如砂土)
- 变水头试验:适用于渗透性较小的土(如黏性土)
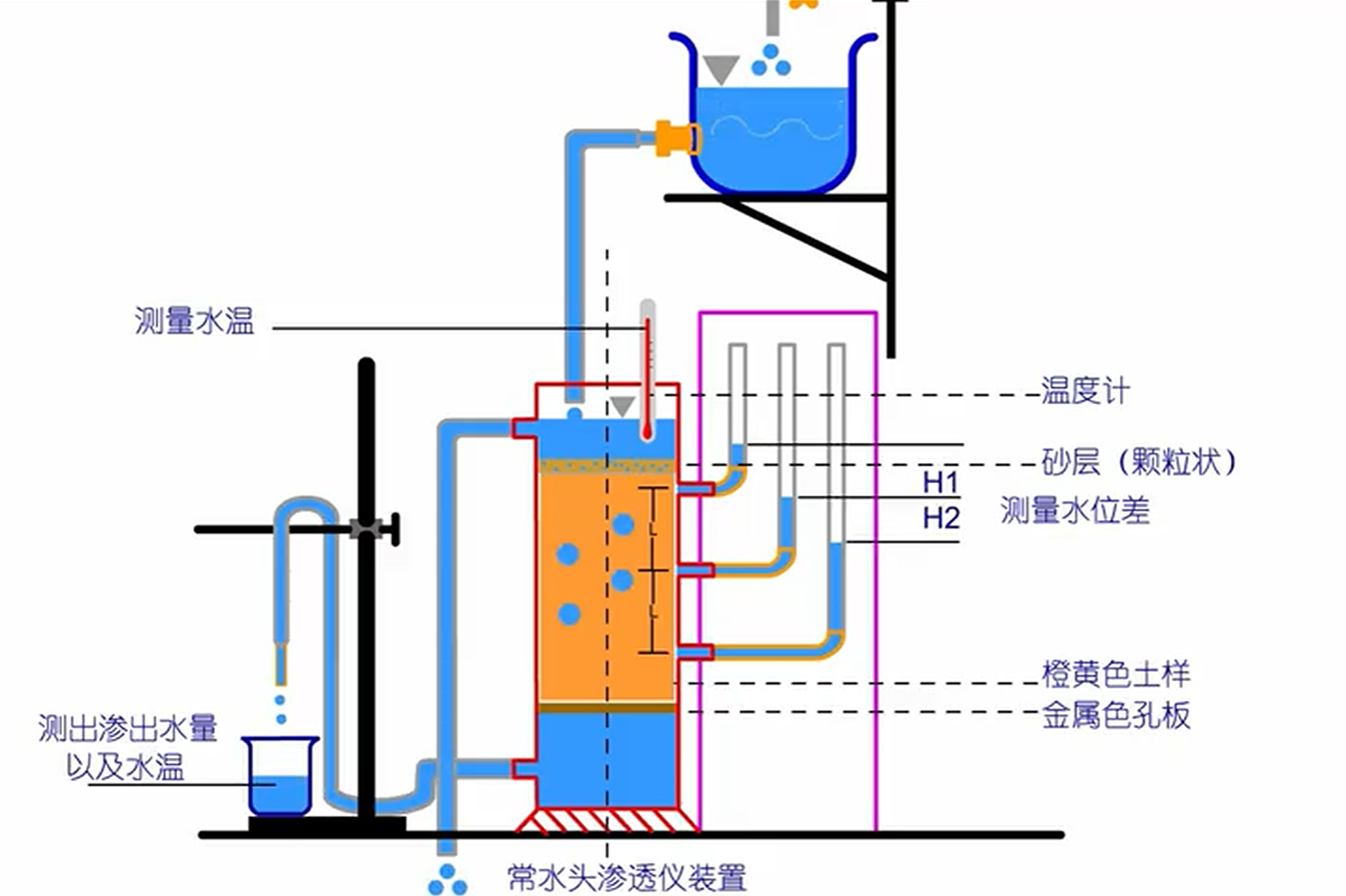
图2.2 实验室渗透系数测定装置
2.3.2 常水头试验计算
常水头试验中渗透系数的计算公式:
k = QL / (Aht)
其中:
- Q:时间t内的渗水量(m³)
- L:渗流路径长度(m)
- A:试样的截面积(m²)
- h:水头差(m)
- t:时间(s)
2.3.3 变水头试验计算
变水头试验中渗透系数的计算公式:
k = 2.3aL / (A(t2-t1)) · lg(h1/h2)
其中:
- a:测压管的截面积(m²)
- L:渗流路径长度(m)
- A:试样的截面积(m²)
- t1, t2:时间(s)
- h1, h2:t1, t2时刻的水头差(m)
2.3.4 现场测定方法
现场测定渗透系数的方法主要有:
- 抽水试验
- 压水试验
- 注水试验
2.4 渗透系数的影响因素
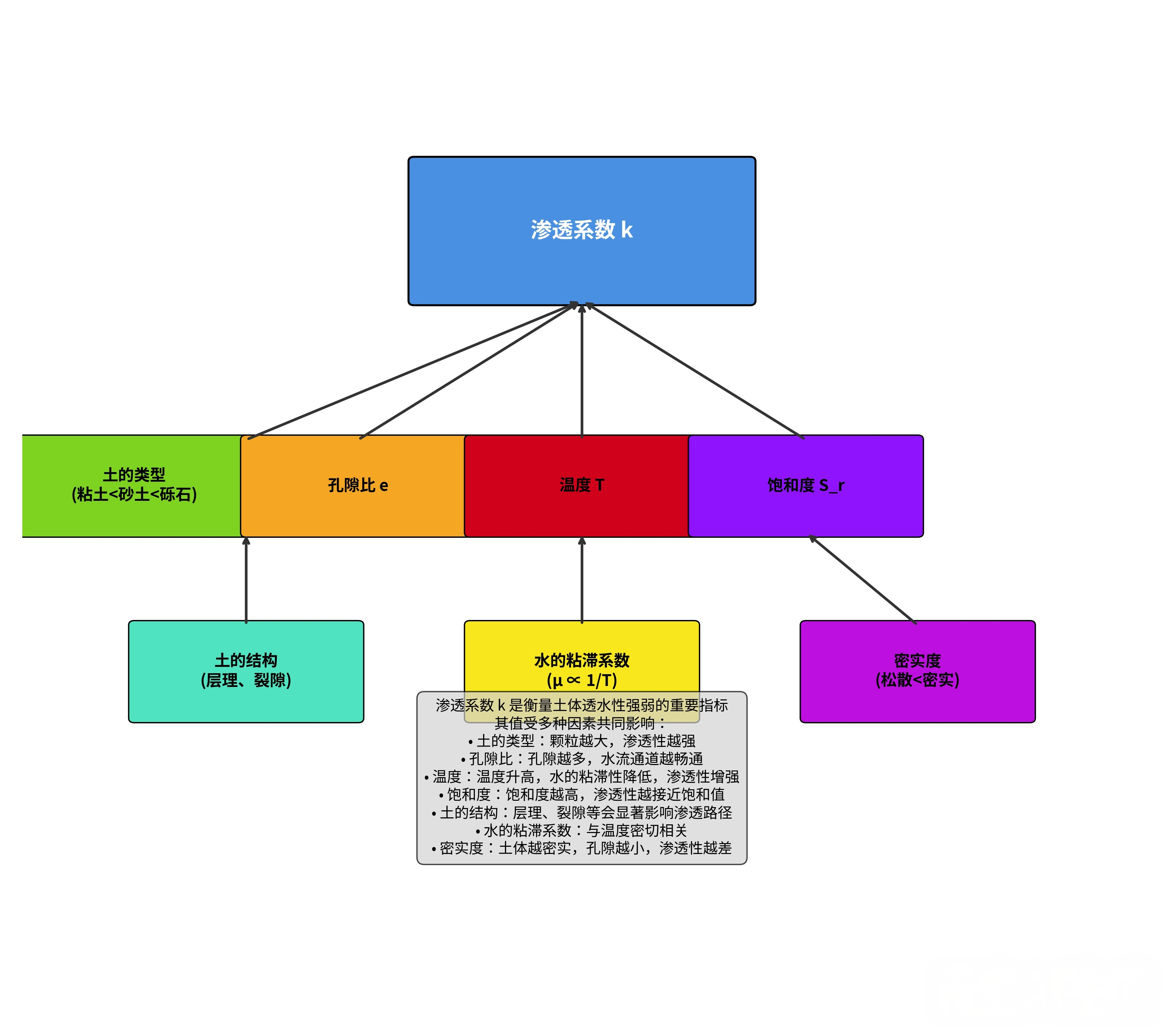
图2.3 不同土类的渗透系数范围
2.4.1 土的性质影响
- 粒径大小与级配:颗粒越大,级配越好,渗透系数越大
- 孔隙比:孔隙比越大,渗透系数越大
- 矿物成分:黏性土中亲水矿物(如蒙脱石)含量越高,渗透系数越小
- 土的结构:絮状结构的黏性土渗透系数较小
2.4.2 水的性质影响
- 温度:水温越高,粘滞系数越小,渗透系数越大
- 水中杂质:水中溶解或悬浮的物质会影响渗透系数
k_T = k_20 · (ν_20 / ν_T)
其中:
- k_T:温度T时的渗透系数(m/s)
- k_20:温度20℃时的渗透系数(m/s)
- ν_20:20℃时水的运动粘滞系数(m²/s)
- ν_T:温度T时水的运动粘滞系数(m²/s)
2.5 二维渗流与流网
2.5.1 渗流的基本方程
对于各向同性的均质土,二维渗流的连续方程和运动方程:
∂²h/∂x² + ∂²h/∂y² = 0
这是拉普拉斯方程,表示稳定渗流条件下,水头分布必须满足的条件。
2.5.2 流网的概念
流网是由流线和等势线组成的网格系统:
- 流线:表示水流的路径,流线上任一点的切线方向与该点的渗流方向一致
- 等势线:连接水头相等的点的线,等势线上各点的测压管水头相同
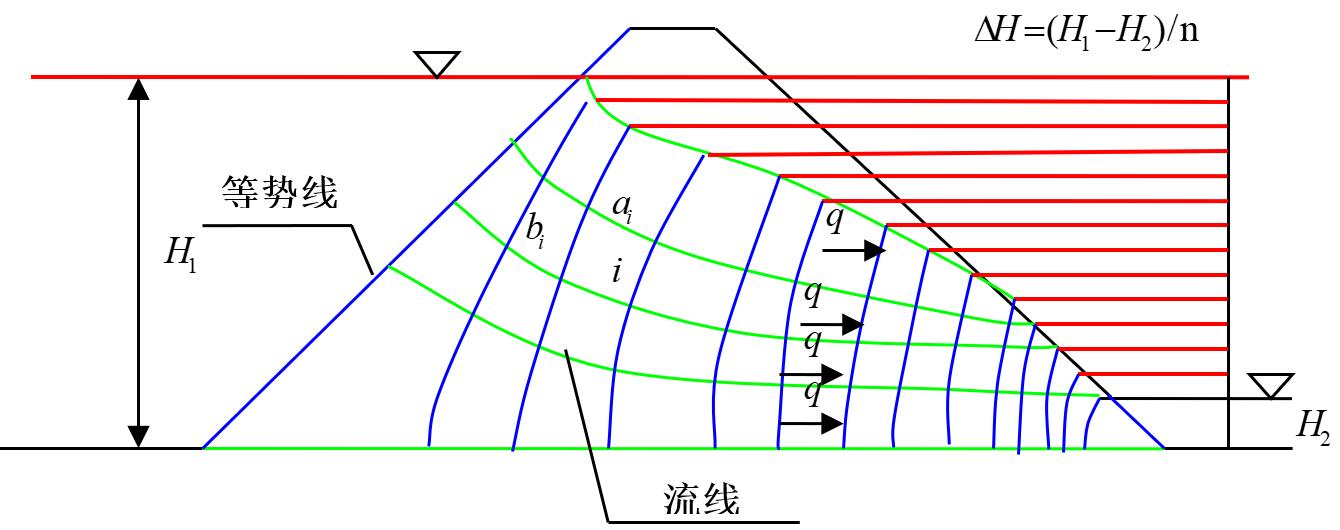
图2.4 流网的基本结构示意图
2.5.3 流网的绘制
流网绘制的基本步骤:
- 确定渗流区域的边界条件
- 根据边界条件绘制初步的流线和等势线
- 检查流线与等势线是否正交,网格是否近似正方形
- 调整和修正,直到满足流网的基本条件
2.5.4 流网的应用
利用流网可以:
- 计算渗流量
- 确定渗流速度
- 分析渗透稳定性
- 计算渗透压力

图2.5 渗流过程中的渗透力作用示意图
知识拓展
在复杂的渗流问题中,也可以使用数值方法(如有限元法、有限差分法)求解渗流场。
本章小结
- 土的渗透性是指水流过土中孔隙的难易程度,用渗透系数k表示
- 达西定律描述了层流状态下渗流速度与水力梯度的线性关系
- 渗透系数可以通过室内试验(常水头、变水头)和现场试验测定
- 渗透系数受土的性质和水的性质等多种因素影响
- 流网是分析二维渗流问题的有效工具