3.1 概述
土中应力计算是土力学中的重要内容,对于分析地基的沉降、强度和稳定性具有重要意义。
3.1.1 土中应力的分类
- 自重应力:由土本身的重量引起的应力
- 附加应力:由建筑物等外部荷载引起的应力
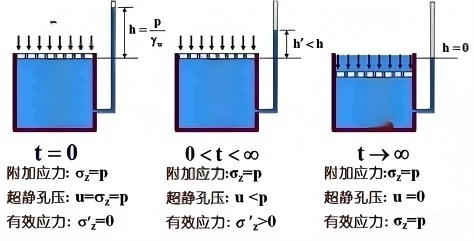
3.1.2 有效应力原理
土中的总应力σ等于有效应力σ'与孔隙水压力u之和:
σ = σ' + u
有效应力是控制土的变形和强度的关键因素。
3.2 自重应力计算
3.2.1 均质土的自重应力
对于均质土,任意深度z处的竖向自重应力为:
σ_cz = γz
其中:
- γ:土的天然重度(kN/m³)
- z:计算点深度(m)
3.2.2 成层土的自重应力
对于成层土,深度z处的竖向自重应力为各层土自重应力之和:
σ_cz = Σ(γ_i h_i)
其中:
- γ_i:第i层土的重度(kN/m³)
- h_i:第i层土的厚度(m)
3.2.3 地下水位对自重应力的影响
地下水位以下的土应采用有效重度(浮重度)计算自重应力:
γ' = γ_sat - γ_w
其中:
- γ_sat:土的饱和重度(kN/m³)
- γ_w:水的重度(kN/m³),通常取10kN/m³
注意
地下水位的升降会引起自重应力的变化,从而导致地基的沉降或隆起。
3.3 基底压力计算
3.3.1 中心受压基础的基底压力
对于中心受压的矩形基础,基底平均压力为:
p = (F + G) / A
其中:
- F:上部结构传至基础顶面的竖向力(kN)
- G:基础自重及其上回填土重(kN)
- A:基础底面面积(m²)
3.3.2 偏心受压基础的基底压力
对于单向偏心受压的矩形基础,基底压力分布为梯形或三角形:
p_max,min = (F + G)/A ± (M/W)
其中:
- M:弯矩(kN·m)
- W:基础底面的抵抗矩(m³)
当偏心距e = M/(F+G) ≤ b/6时,基底压力分布为梯形:
p_max,min = (F + G)/A (1 ± 6e/b)
当e > b/6时,基底压力分布为三角形:
p_max = 2(F + G)/(3la)
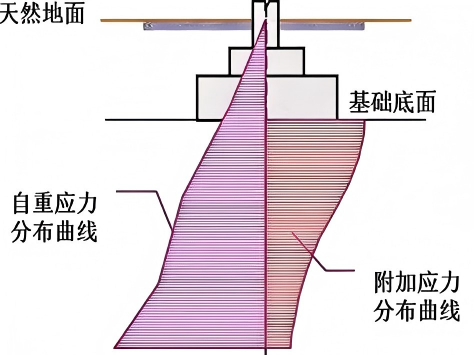
3.3.3 基底附加压力
基底附加压力是指建筑物荷载在地基中引起的额外应力:
p_0 = p - σ_cz
其中:
- p:基底压力(kPa)
- σ_cz:基底处原有自重应力(kPa)
3.4 地基中的附加应力
3.4.1 集中荷载作用下的附加应力
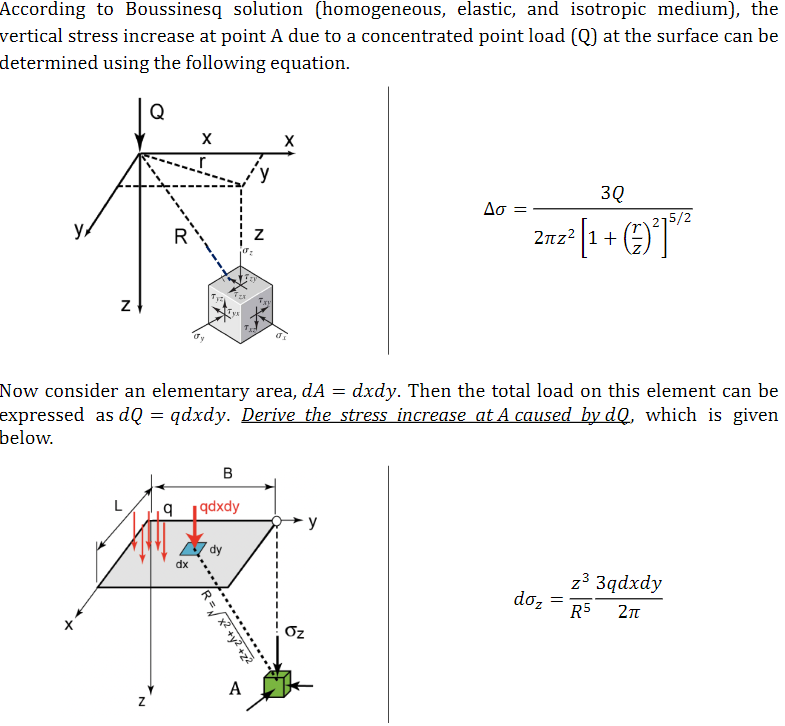
布辛涅斯克(Boussinesq)解:在均质、各向同性的弹性半空间表面作用一个竖向集中力P时,土中任意点M(x,y,z)处的附加应力为:
σ_z = (3P)/(2πz²) · [1/(1+(r/z)²)]^(5/2)
其中:
- P:集中力(kN)
- z:计算点深度(m)
- r:计算点到集中力作用线的水平距离(m)
3.4.2 均布矩形荷载作用下的附加应力
对于均布矩形荷载,角点下任意深度z处的附加应力为:
σ_z = α_c · p_0
其中:
- p_0:基底附加压力(kPa)
- α_c:角点应力系数,与l/b和z/b有关(l为矩形长边,b为矩形短边)
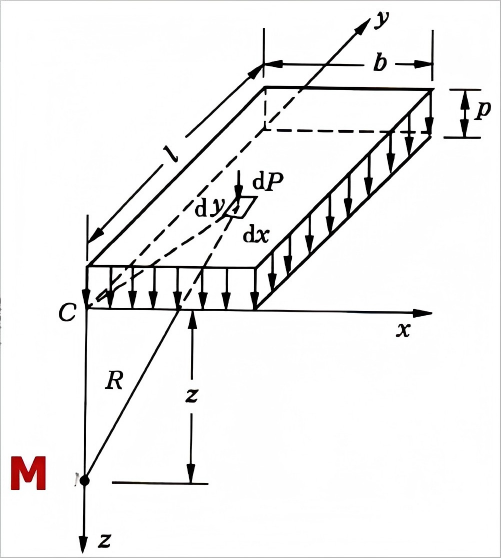
3.4.3 均布条形荷载作用下的附加应力
对于均布条形荷载,通过条形中心线上任意深度z处的附加应力为:
σ_z = α_s · p_0
其中:
- p_0:基底附加压力(kPa)
- α_s:条形荷载应力系数,与z/b有关(b为条形基础宽度)
3.4.4 附加应力的分布规律
- 附加应力随深度的增加而减小
- 附加应力在水平方向上的分布范围随深度增加而扩大
- 相同荷载下,基础尺寸越大,附加应力影响深度越大

知识拓展
在实际工程中,还可以使用应力叠加原理计算复杂荷载作用下的附加应力分布。
3.5 应力路径
3.5.1 应力路径的概念
应力路径是指在荷载作用下,土中某点的应力状态随时间变化的轨迹,通常用主应力差σ1-σ3和平均有效应力p'等参数表示。
3.5.2 应力路径的表示方法
常用的应力路径表示方法:
- p'-q'平面(p'=(σ1'+σ3')/2,q'=σ1'-σ3')
- τ-σ'平面(σ'为法向有效应力,τ为剪应力)
- Kp和Kf线(Kp为破坏线,Kf为临界状态线)
3.5.3 典型应力路径
- 三轴排水试验:p'增加,q'增加
- 三轴不排水试验:p'保持不变,q'增加
- 侧限压缩试验:p'增加,q'=0
3.5.4 应力路径的工程应用
- 分析土的强度和变形特性
- 预测地基的沉降和稳定性
- 指导基础设计和施工
本章小结
- 土中应力分为自重应力和附加应力
- 有效应力原理是土力学的重要原理,有效应力控制土的变形和强度
- 自重应力计算需考虑成层土和地下水位的影响
- 基底压力计算分为中心受压和偏心受压两种情况
- 地基附加应力计算可采用布辛涅斯克解、角点法等方法
- 应力路径可用于分析土的应力状态变化过程